本帖最后由 602723113 于 2020-3-19 19:38 编辑

[Tutorial][数学向]从零开始的MC特效(六 | 坐标系的旋转)
我胡汉三又回来啦！
目录:
  • 导读
  • Location点的旋转
  • 坐标系的修正与在玩家背部建立坐标系
  • 制作简易翅膀
导读
  • 本教程需要读者有一定的空间想象能力(因为我也懒得画图了233)
  • 本教程使用的 PaperSpigot1.12.2-R0.1-SNAPSHOT 核心
  • 在阅读之前请确保你具有高中数学必修4和和Java基础的知识


  • <To初中生>: 如果你是初中的话，别慌，你有趋向的概念就可以读懂本教程(应该吧...)
  • <To高中生>: 如果你还未学到关于上面的那本书，别慌学到了再来看也行233 (雾
  • <To大学生>: 没什么好说的...



Location点的旋转
首先我们引入平面上点围绕另一个点进行旋转的公式 (数学上) 平面中，一个点(x,y)绕任意点(x0,y0)逆时针旋转a度后的坐标
  1. dx = (x - x0)*cos(a) - (y - y0)*sin(a) + x0 ;
  2. dy = (x - x0)*sin(a) + (y - y0)*cos(a) + y0 ;
复制代码
那么我们写入代码看看是怎么样的
  1. /**
  2. * 在二维平面上利用给定的中心点逆时针旋转一个点
  3. *
  4. * @param location 待旋转的点
  5. * @param angle    旋转角度
  6. * @param point    中心点
  7. * [url=home.php?mod=space&uid=491268]@Return[/url] {[url=home.php?mod=space&uid=41191]@link[/url] Location}
  8. */
  9. public static Location rotateLocationAboutPoint(Location location, double angle, Location point) {
  10.     double radians = Math.toRadians(angle);
  11.     double dx = location.getX() - point.getX();
  12.     double dz = location.getZ() - point.getZ();

  14.     double newX = dx * Math.cos(radians) - dz * Math.sin(radians) + point.getX();
  15.     double newZ = dz * Math.cos(radians) + dx * Math.sin(radians) + point.getZ();
  16.     return new Location(location.getWorld(), newX, location.getY(), newZ);
  17. }
复制代码
总所周知，在mc坐标内，玩家走动的二维平面，其实是影响x轴和z轴的内容，所以我们上方的代码就套用x，z
坐标系的修正与在玩家背部建立坐标系

在我们之前的教程中，我们都会发现，我们在做一些让特效出现在玩家面前时，会出现特效出现在另外一边，这其实就是我们没有经过玩家朝向的修正，而发生的情况，比如下面这一张图

那么我们可以重新建立一个修正过后的坐标系，用的方法就是利用Location点的旋转
  1. import org.bukkit.Location;

  3. /**
  4. * 自动修正在平面上的粒子朝向
  5. *
  6. * [url=home.php?mod=space&uid=1231151]@author[/url] Zoyn
  7. */
  8. public class PlayerFixedCoordinate {

  10.     private Location zeroDot;
  11.     private double rotateAngle;

  13.     public PlayerFixedCoordinate(Location playerLocation) {
  14.         // 旋转的角度
  15.         rotateAngle = playerLocation.getYaw();
  16.         zeroDot = playerLocation.clone();
  17.         zeroDot.setPitch(0);
  18.         // 重设仰俯角, 防止出现仰头后旋转角度不正确的问题
  19.     }

  21.     public Location getZeroDot() {
  22.         return zeroDot;
  23.     }

  25.     public Location newLocation(double x, double z) {
  26.         return rotateLocationAboutPoint(zeroDot.clone().add(-x, 0, z), rotateAngle, zeroDot);
  27.     }

  29.         /**
  30.      * 在二维平面上利用给定的中心点逆时针旋转一个点
  31.      *
  32.      * @param location 待旋转的点
  33.      * @param angle    旋转角度
  34.      * @param point    中心点
  35.      * @return {@link Location}
  36.      */
  37.     public static Location rotateLocationAboutPoint(Location location, double angle, Location point) {
  38.         double radians = Math.toRadians(angle);
  39.         double dx = location.getX() - point.getX();
  40.         double dz = location.getZ() - point.getZ();

  42.         double newX = dx * Math.cos(radians) - dz * Math.sin(radians) + point.getX();
  43.         double newZ = dz * Math.cos(radians) + dx * Math.sin(radians) + point.getZ();
  44.         return new Location(location.getWorld(), newX, location.getY(), newZ);
  45.     }
  46. }
复制代码
首先我们来分析这个类是怎么写的，首先我们要旋转一个点，就需要旋转的角度，那么这时候 location 里的 yaw 就可以帮助我们完成这个工作，所以我在构造器里将 yaw 记录为 rotateAngle

之后我们看newLocation这个方法，需要填入两个参数分别是 x, y （为了方便理解，我其实直接将其设计为数学上的平面直角坐标系（右手坐标系））

而我们在看
  1. zeroDot.clone().add(-x, 0, z)
复制代码
这行代码, 首先它是 rotateLocationAboutPoint 方法里的待旋转的点，那么我们为什么要add呢？ 因为啊, zeroDot 就是我们坐标系的原点，经过add之后就可以得到新的x，y了，
比如说，zeroDot是(0, 0)，方法填入3, 2, 那么add完之后就得到 (3, 2) 这个点

那么为什么是-x呢？？？
因为啊，在Mc中的坐标系是遵循左手坐标系来设计的，所以它的x轴我们要乘以一个-1才能按照我们平常理解的右手坐标系来绘图。
现在我们套用上这个修复过的坐标系来看看效果

完整代码:
  1. Player player = ........
  2. PlayerFixedCoordinate coordinate = new PlayerFixedCoordinate(player.getLocation());

  4. double radius = 10;
  5. for (double t = -1; t <= 1; t += 0.001) {
  6.     double x = radius * Math.sin(t) * Math.cos(t) * Math.log(Math.abs(t));
  7.     double y = radius * Math.sqrt(Math.abs(t)) * Math.cos(t);

  9.     Location loc = coordinate.newLocation(x, y);
  10.     loc.getWorld().spawnParticle(Particle.FIREWORKS_SPARK, loc, 1, 0, 0, 0, 0);
  11. }
复制代码
下面分享一个PlayerBackCoordinate为了让读者能够举一反三，希望读者能够自行添加 z 轴的变化（思考：z轴的变化在右手坐标系中是如何变化，又应该如何将其转换至MC坐标系内）
绘图思考可以参照这张图：

  1. import org.bukkit.Location;

  3. /**
  4. * 将玩家背后转换为一个平面直角坐标系
  5. *
  6. * @author Zoyn
  7. */
  8. public class PlayerBackCoordinate {

  10.     private Location zeroDot;
  11.     private double rotateAngle;

  13.     public PlayerBackCoordinate(Location playerLocation) {
  14.         // 旋转的角度
  15.         rotateAngle = playerLocation.getYaw();
  16.         zeroDot = playerLocation.clone();
  17.         zeroDot.setPitch(0); // 重设仰俯角
  18.         zeroDot.add(zeroDot.getDirection().multiply(-0.3)); // 使原点与玩家有一点点距离
  19.     }

  21.     public Location getZeroDot() {
  22.         return zeroDot;
  23.     }

  25.     public Location newLocation(double x, double y) {
  26.         return rotateLocationAboutPoint(zeroDot.clone().add(-x, y, 0), rotateAngle, zeroDot);
  27.     }

  29.         /**
  30.      * 在二维平面上利用给定的中心点逆时针旋转一个点
  31.      *
  32.      * @param location 待旋转的点
  33.      * @param angle    旋转角度
  34.      * @param point    中心点
  35.      * @return {@link Location}
  36.      */
  37.     public static Location rotateLocationAboutPoint(Location location, double angle, Location point) {
  38.         double radians = Math.toRadians(angle);
  39.         double dx = location.getX() - point.getX();
  40.         double dz = location.getZ() - point.getZ();

  42.         double newX = dx * Math.cos(radians) - dz * Math.sin(radians) + point.getX();
  43.         double newZ = dz * Math.cos(radians) + dx * Math.sin(radians) + point.getZ();
  44.         return new Location(location.getWorld(), newX, location.getY(), newZ);
  45.     }
  46. }
复制代码
上方代码的使用：实例1：在玩家后背绘制一个圆
  1. Player player = (Player) sender;
  2. PlayerBackCoordinate coordinate = new PlayerBackCoordinate(player.getLocation().add(0, 1.6D, 0));

  4. for (int angle = 0; angle < 360; angle++) {
  5.     double radians = Math.toRadians(angle);
  6.     double x = Math.cos(radians);
  7.     double y = Math.sin(radians);

  9.     Location loc = coordinate.newLocation(x, y);
  10.     loc.getWorld().spawnParticle(Particle.FLAME, loc, 1, 0, 0, 0, 0);
  11. }
复制代码
具体效果：


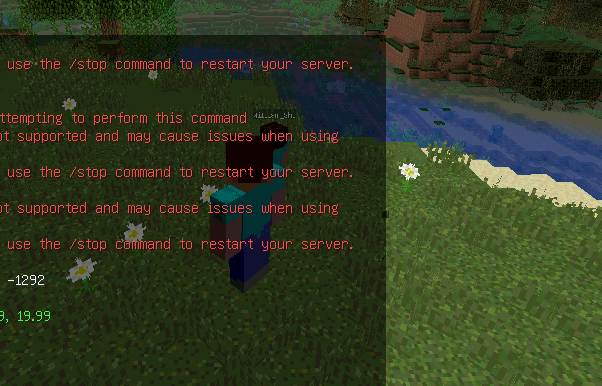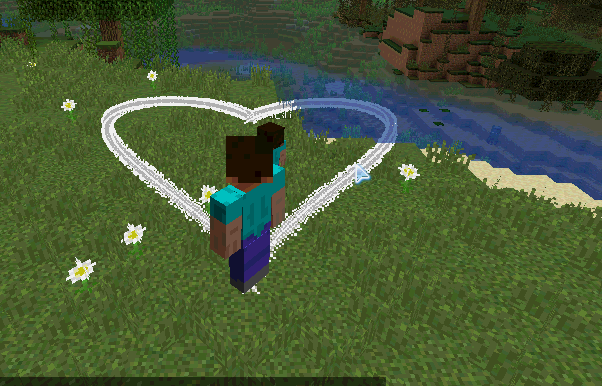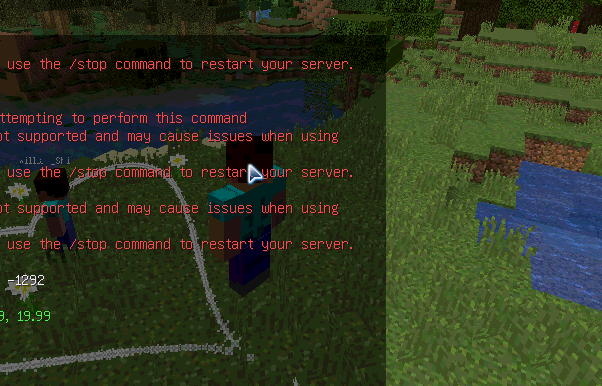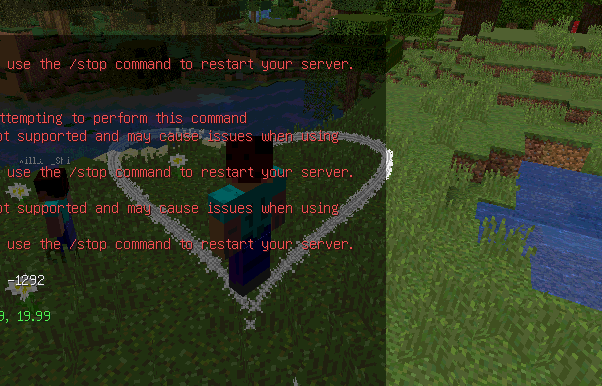
制作简易翅膀
不说这么多，直接上代码好吧，用的就是上面的代码
  1. Player player = (Player) sender;
  2. PlayerBackCoordinate coordinate = new PlayerBackCoordinate(player.getLocation().add(0, 1.5D, 0));

  4. for (double angle = 0; angle <= 135; angle++) {
  5.     double x = Math.toRadians(angle);
  6.     double y = Math.sin(2 * x);

  8.     Location loc = coordinate.newLocation(x, y);
  9.     loc.getWorld().spawnParticle(Particle.VILLAGER_HAPPY, loc, 1, 0, 0, 0, 0);
  10. }

  12. for (double angle = -135; angle <= 0; angle++) {
  13.     double x = Math.toRadians(angle);
  14.     double y = Math.cos((2 * x) + (Math.PI / 2));

  16.     Location loc = coordinate.newLocation(x, y);
  17.     loc.getWorld().spawnParticle(Particle.VILLAGER_HAPPY, loc, 1, 0, 0, 0, 0);
  18. }

  20. coordinate = new PlayerBackCoordinate(player.getLocation().add(0, 1, 0));
  21. double radius = 0;
  22. for (double angle = 0; angle <= 3 * 360; angle++) {
  23.     double radians = Math.toRadians(angle);
  24.     double x = radius * Math.cos(radians);
  25.     double y = radius * Math.sin(radians);

  27.     Location loc = coordinate.newLocation(x, y);
  28.     loc.getWorld().spawnParticle(Particle.FIREWORKS_SPARK, loc, 1, 0, 0, 0, 0);
  29.     radius += 0.001;
  30. }
复制代码
具体效果:

结语
是的这个教程又开始更新了，就当做没事拿来玩玩的了，毕竟上了大学，还是可以拿线性代数来学以致用的嘛嘻嘻嘻。此外我想开一个ParticleLib的坑，专门来制作这类特效，希望各位看官可以多多支持

看情况更新 —— 撰写: 一个来自已经上了带学的大一新生 2020/3/8

[groupid=1701]Complex Studio[/groupid]